今日心得:同一组多项式公式,fibonacci多项式输出是galois多项式输出的反向序列;
galois宜使用normal POLY表示法,fibonacci宜使用Koopman POLY表示法。

对于给定POLY,galois多项式使用reciprocal POLY,即可输出等效于使用Koopman POLY的fibonacci多项式的输出序列。
举例说明:
G(x) = x^7 + x^6 + 1
其POLY的四种格式为:
| Type | Poly status |
| Normal | 7b(1)100_0001 |
| Reverse | 7b100_0001(1) |
| Koopman | 7b110_0000(1) |
| Reciprocal | 7b(1)000_0011 |
该多项式的finonacci电路使用Koopman POLY,输出序列即为最常见的prbs7 pattern;
使用normal POLY给到galois电路,则输出与prbs7 pattern方向相反的序列;
使用reciprocal POLY给到galois电路,则输出与prbs7 pattern相同的序列。
另有二则在网上冲浪时的启发:
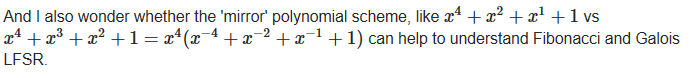
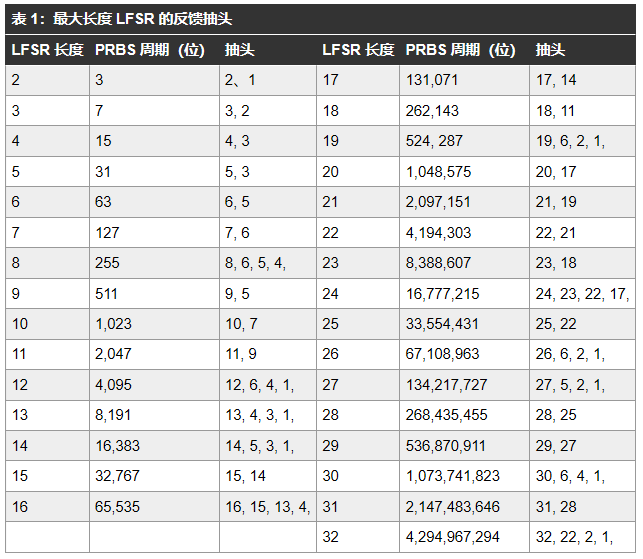
最后,汇总常用option,做了一个通用的多项式扰码模块。
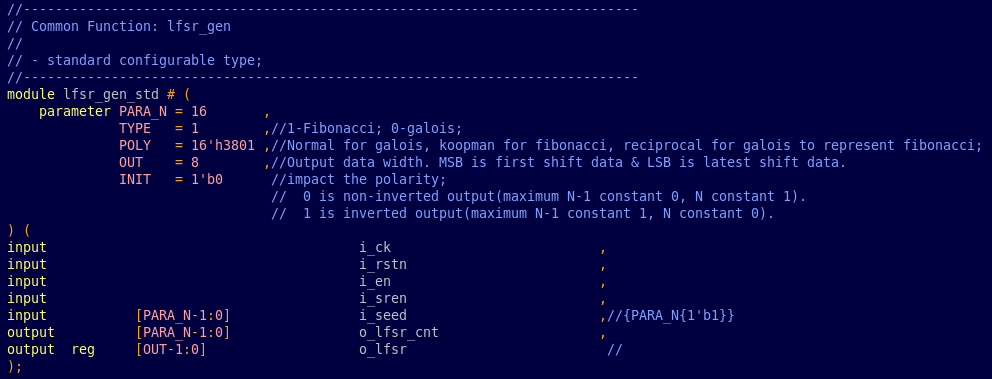
TBD:后面会综合做对比,看看面积是否还能优化。
